(二)误差与准确度
准确度指实验测定值(X)与真实值(T)之间的符合程度,常用误差的大小来衡量。误差的绝对误差和相对误差。绝对误差指测定值与真实值之间的差值,用“E”来表示。相对误差指的是绝对误差占真实值的百分率,用“%RE”表示。即
绝对误差:E=X-T
相对误差:(%)RE=E/T×100
误差越小,表示实验结果与真实值越接近,测定的准确度也越高。而与绝对误差相比,相对误差更能反映出实验结果的准确程度。因此在滴定分析中一般多采用相对误差来表示测量的准确度。
(三)偏差与精密度
在实际工作中真实值往往是不知道的,此时便不好用误差来评价分析结果,通常用相同条件下多次测定结果的平均值(X) 来代替真实值,用偏差来衡量所得结果的精密试。
精密度指多次重复测定的结果相互接近的程度,是保证准确度的前提。偏差是指各次测定的结果和平均值之间的差值。偏差越小,精密度越高。
偏差分为绝对偏差(d)、相对偏差(Rd)、平均偏差(d)和相对平均偏差 (Rd),它们的表达式为:
绝对偏差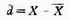
相对偏差
平均偏差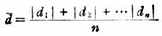
相对平均偏差
式中d1,d2…dn为第1,2…n次测量结果的偏差,X为单次测定值,x 为测定平均值。
对于一般的滴定分析来讲,因测定次数不多,故常用相对平均偏差来表示实验的精密度。