5.结果分析 队列研究是发生率的研究,包括疾病发生率与死亡发生率。以死亡作终点的队列研究比以发病作终点的为多,这是因为死亡的确定比发病的确定容易。
队列研究的结果,可以用来计算所研究疾病在随访期间的发病率或死亡率及各种专率。通过对暴露组与非暴露组的率或不同剂量的暴露组的率的比较,或暴露组的率与全人群的率比较,便可检验病因假设;对可疑病因的暴露与疾病(死亡)是否存在联系;联系强度如何;是否是因果联系。
(1)率的计算
1)累积发病率(cumulative incidence rate,CI):某一固定人群在一定时期内某病新发生例数(D)与时期开始总人数(N)之比(表4-7,公式4-7)。也就是一般所说的发病率。随访期越长,则病例发生越多,所以CI表示发病率的累积影响。CI又是平均危险度的一个指标,也就是一个人在特定时期内发生该病的概率。
CI=C/N
(式4-7)
2)发病密度(incidence density,ID):当队列是一个动态人群时,观察人数变动较大(因失访、迁移、死于他病、中途加入等),应该用发病密度来测量发病情况(表4-8,公式4-8)。发病密度是一定时期内的平均发病率。其分子仍是一个人群在期内新发生的例数(D),分母则是该人群的每一成员所提供的人时的总和。所谓人时(person-time,PT)是观察人数乘以随访单位时间的积。发病密度即说明了该人群发生的新病例数,又说明该人群的大小和发生这些例数所经历的时间。时间单位常用年,故又称人年数(person-years)。一定的人时(人年)数可来自不同的人数与不同的观察时间,例如100人年可来自100人观察一年,或50人观察2年,或200人观察0.5年。
表4-7 累积发病率的计算
| 级别 | 发病数 | 未发病数 | 发病率 |
| 暴露组 | α | b | α/(α+b) |
| 非暴露组 | c | d | c/ c+d) |
| 合计 | α+c(=D) | D/(α+b+c+d) |
表4-8 发病密度的计算
|
组别 |
发病数 |
人年数 |
发病密度 |
|
暴露组 |
α |
PT1 |
α/PT1 |
|
非暴露组 |
c |
PT0 |
c/PT0 |
|
合计 |
a+c(=D) |
PT |
D/PT |
ID=D/PT
(式4-8)
人年数的算法:①固定人群,即封闭人群,人年数是每一个成员的具体观察年数的总和。每一成员的观察年数是从观察开始算起到终点事件出现或研究结束时经过的年数(月数、周数、以至日数均可折算为年数);②动态人群,如果不知道每一成员进入与退出的具体时间,就不能直接计算人年数。但如随访期间人数与年龄基本保持稳定,则可用平均人数采以观察年数得到总人年数。平均人数取得相邻两时段人数之平均数或年中人数,例如表4-9(节录Doll与Hill关于吸烟与肺癌关系的队列研究第2报)。
表4-9 人年数的计算实例
|
年龄(岁) |
观察人数 |
人年数 | |||||
|
1951.11.01 |
1952.11.01 |
1953.11.01 |
1954.11.01 |
1955.11.01 |
1956.04.01 | ||
|
35~ |
8886 |
9149 |
9287 |
9414 |
9710 |
9796 |
41211 |
|
45~ |
7117 |
7257 |
7381 |
7351 |
7215 |
7191 |
32156 |
|
55~64 |
4049 |
4212 |
4375 |
4601 |
5057 |
5243 |
19909 |
|
合计 |
20097 |
20618 |
21043 |
21366 |
21982 |
22230 |
93276 |
例如,表4-9中“35~”岁组的人年数=(8886+9149)÷2+(9149+9287)÷2+(9287+9414)÷2+(9414+9710)÷2+(9710+9796)÷2×5/12=41211;③各人随访年数不同,可先算出各人随访人年数,再计算总人年数;而且因为随访期内各人的年龄在增长,到一定日期(某岁生日)年龄超过原属年龄组上限时,应计入下一年龄组的人数。所以可以算出各年龄组的总人年数以及不同年份(日历年calendar year)的总人年数,结合同年龄组或同年份发生的病例数,即可算出各年龄组或年份的发病率(发病密度)。确切算法要根据每一成员的出生年、月、日和开始与终止观察日期而动态地计算,可借助计算机。实际上还可用近似法:开始与终止观察年份各算0.5年,同一年开始与终止的算0.25年,开始与终止年份之间,每年算1年。
人时率的标准误、显著性检验和分层分析方法,与通常以人数为分母的率所用的不同,本书从略。
(2)联系的测量:研究某种暴露与疾病或死亡的联系的基本方法是比较暴露组与未暴露组的发病率或死亡率,也就是计算出这些率的差或比。
1)率差:暴露组的发病率或死亡率与未暴露组同种率之差。说明由于暴露增加或降低的发病率或死亡率。有人称率差为归因危险度(attributable risk)也有人认为称为超额(或超常)危险度(excess risk)比较合适,因其不含因果联系的暗示。
2)人群归因危险度(population attributable risk,PAR)率差与相对危险度都说明暴露的生物学效应,但不能说明其对一个人群的危险程度或消除这种因素后可能使发病率或死亡率降低的程度,或即暴露的社会效应。说明这种效应的一个指标是人群归因危险度,它说明某一人群(包括暴露者与非暴露者)的某病发病(或死亡)率中可归因于该暴露的部分,用所占比例或分数表示,如下式:

(式4-9)
式中It=全人群的发病率,I0=未暴露组的发病率。PAR又称病因分数(分值)(etiologic fraction EF),也可用百分比表示,称为人群归因危险度百分比。
①病例对照研究的PAR计算:从暴露的相对危险度(见下文“率比”)和人群对某因子的暴露率(Pe),可算出PAR。如果病例对照研究中对照组的暴露率可以代表人群暴露率,则可用下式:
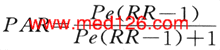
(式4-10)
如以百分比表示,也称为人群归因危险度百分比(population attributable risk percent-age,PARP)。
②队列研究用人时(发病密度)数据时的指标计算:
|
暴露 |
非暴露 |
合计 | |
|
病例数 |
α |
b |
m |
|
人年数 |
c |
d |
PT |

人群归因危险度的大小取决于危险因子(病因)的相对危险度和人群暴露比例(表4-10)。例如,据Doll与Peto研究(1981),1978年美国癌症死亡中的25%~40%(平均30%,约12万人)可归因于吸烟,而同年归因于职业因素的癌症死亡只占2%~8%(平均4%)。两者相差这么悬殊是因为人群的吸烟率很高而暴露于职业性致癌因素的人相对很少。
表4-10 人群归因危险度百分比与相对危
险度(RR)和人群暴露率(Pe)的关系
|
Pe |
RR | |||
|
1.5 |
2 |
5 |
10 | |
|
0.01 |
0.5 |
1 |
4 |
8 |
|
0.05 |
2 |
5 |
17 |
31 |
|
0.10 |
5 |
9 |
29 |
47 |
|
0.25 |
11 |
20 |
50 |
69 |
|
0.5 |
20 |
33 |
67 |
82 |
|
0.9 |
31 |
47 |
78 |
89 |
计算实例:表4-11是一项关于血清胆固醇水平与发生冠心病(CHD)的危险度的6年随访研究结果。这是从1948年开始的著名的美国Framingham心脏病队列研究的一部分(此研究后来以当初成员的后代为对象,继续进行)。
表4-11 40~59岁男子按初始血清胆固醇水平分组的冠心病6年发生情况
| 血清胆固醇(mg/dl) | 人数 | 病倒数 | 危险度 | 平均年发病率 | 相对危险度 | 率差 |
|
<210 |
454 |
16 |
0.0352 |
0.0059 |
1.00 |
0.0000 |
|
210~ |
455 |
29 |
0.0637 |
0.0106 |
1.81 |
0.0285 |
|
≥245 |
424 |
51 |
0.1203 |
0.0200 |
3.39 |
0.0851 |
|
合计 |
1333 |
96 |
0.0720 |
0.0120 |
- |
- |
转引自Feinleib与Detels,1985
表中,危险度系用式4-7计算,也就是累积发病率,说明6年随访期间发生CHD的危险度,除以6得年平均发病率。胆固醇的浓度以观察开始时检查的结果为准,相对危险度的计算以<210mg/dl(约合5.439mmol/L)组的危险度为1。率差或超额危险度系0.0352与其他两组危险度之差,表示不同程度的暴露所增加的危险度。如以<210mg/dl组的发病率作为未暴露组的发病率,即Io=0.0059,以≥245mg/dl(约合6.3455mmol/L)组为暴露组,则Io=0.0200,用式4-9算出PAR=(0.0120-0.0059)/0.0120=0.51。这可解释为如所有40~59岁男子的血清胆固醇浓度都能控制在210mg/dl以下时,该人群的CHD发病率将可降低51%。
3)率比与相对危险度(relative risk,RR):队列研究中暴露组的发病率(发病密度)与非暴露组的发病率之比,称为率比。率比、危险度比和比数比(OR)在危险度不高时(少见病)三者的值几乎相等,都可称为相对危险度。
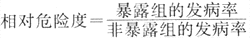
(式4-11)
如以死亡率为终点,则式(4-11)中以死亡率代替发病率。如果按暴露水平分组,以其中某一组的发病率为基准,其他各组的发病率与它的比值也称为相对危险度,例如表4-12中的相对危险度。
相对危险度(RR)无单位,比值范围在0至∞之间。RR=1,表明暴露与疾病无联系;RR<1,表明其间存在负联系(提示暴露是保护因子);反之RR>1时,表明两者存在正联系。比值越大,联系越强。实际上,0与∞只是理论上存在的值,恰恰等于1也不多见。极强的联系既无须用流行病学研究去检测,极弱的联系也不大可能用非实验性的流行病学观察法检测出来。RR与OR的数值所表示的联系强度的解释可参考表4-12。
表4-12 RR或OR与联系强度
| RR或OR |
联系强度 | |
| 0.9~1.0 | 1.0~1.1 | 无 |
| 0.7~0.8 | 1.2~1.4 | 弱 |
| 0.4~0.6 | 1.5~2.9 | 中等 |
| 0.1~0.3 | 3.0~9.0 | 强 |
| <0.1 | 10.0~ | 很强 |
实例:Doll与Hill在1951年向英国注册的59 600名医生通信调查他们的吸烟史。要求他们将自己归入下列3类之一:①现在是吸烟者;②过去吸烟,但已戒掉;③从未习惯性吸烟(即从未“每天吸卷烟1支或与其等量的烟斗丝长达1年”。对现在吸者还询问其开始吸烟时的年龄、现在吸烟量及吸烟方式(指吸入深浅)。对已戒烟者也询问类似问题,但时间限定为刚戒烟前。答复满意者有40710人。以后,在随访期间(男医生为20年,女医生为32年)又函调3次。随访期间多方搜集成员的死亡与迁移动态及死因,力求完全。根据死亡数与随访人年数(表4-9实例)算出各年龄组、不吸烟者、已戒烟者及不同吸烟量者的全死因死亡率。表4-13节录Doll与Peto 1976年发表的对于男医生20年(1951.11~1971.10)随访报告中的表Ⅳ,原表中死因分为40类,可以看出吸烟对健康的全面影响。现节录其中几种重要死因的死亡率。读者可自己计算吸烟的相对危险度(率比),可见吸卷烟者的肺癌死亡率为不吸烟者的10倍,每日吸烟25支或更多者,肺癌死亡率为不吸烟者的25倍,等等。