为了解释别构酶协同效应的机制并推导出动力学曲线的方程式,不少人曾提出过各种模式,各有优缺点,现在主要把Hill模式叙述如下:
Hill模式
在协同结合模式中最早的一种是Hill在1909年提出的,企图解释氧结合至血红蛋白的S形饱和曲线,现称为Hill模式,后来经Atkinson应用于别构酶反应,他设想在这个系统中,n分子的配体(S)能够一步结合到酶上去:
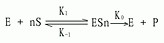
即此反应的总解离常数(K's)由下式决定
|
K'S=[E][S]n/[ESS] |
(6-7) |
而酶的饱和分数
|
YS=每分子酶蛋白上已结合的底物分子数/每分子酶蛋白上底物结合位点的总数 |
(6-8) |
又因总的酶浓度[E0]=[E]+[ES0]
|
故 YS=[ESn]/[E0]=[ESn]/[ESn]+[E] |
(6-9) |
合并式6-7和式6-9,消去[ESn],则
|
YS=[S]n/K'S+[S]n |
(6-10) | ||
|
YSK'S+YS[S]n=[S]n, |
|||
|
YSK'S=(1-Y)[S]n |
(6-11) | ||
|
Ys/1-Ys=[S]n/K'S |
(6-11) | ||
| log |
[YS/(1-YS)] |
=nlog[S]-logK'S | (6-13) |
因此以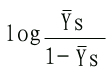 对log[S]作图的话,可得斜率为n,纵轴截距为-logK'S的直线(见下图)。
对log[S]作图的话,可得斜率为n,纵轴截距为-logK'S的直线(见下图)。
因v=k0[ESu],Vm=k0[E0],故
|
|
(6-14) |
将式6-10代入式6-14,即得
|
[S]n/K'S+[S]n=v/Vm |
|
|
Vm[S]n=K'Sv+v[S]n |
(6-15) |
|
(Vm-v)[S]n=K'Sv |
(6-16) |
|
v/Vm-v=[S]n/K'S |
(6-17) |
|
logv/Vm-v=nlog[S]-logK'S |
(6-18) |
式6-13或6-18即为Hill方程式,式6-18如以logv/Vm-v对log[S]作图,也可得一直线(见下图)。
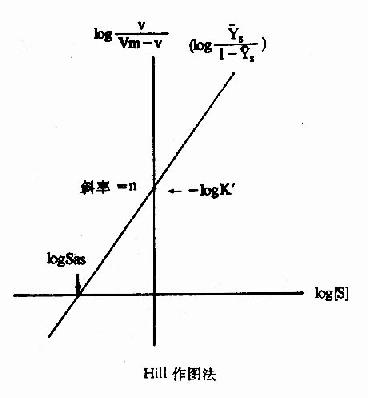
Hill作图法
如v=Vm/2时,式6-19为log1=nlog[S]-logK'S=0(6-19)
此时的[S]即S0.5,故nlogS0.5=logK'5(6-20)式6-18所得的直线斜率为n,纵轴截距为-logk'S,而横轴截距为logK'S/n,即log[S]0.5,但[S0.5]也可在已知logK'S后通过式6?0求取。
上节已述及,S0-5就相当于米曼氏动力学中的Km,当K0《k-1/k1时,可反映别构酶对底物的亲和力,S0.5愈小,亲和力愈大,而K's实际上已与亲和力关系不大,因受到n的影响。故反映底物亲和力的参数,已从非别构酶的Km一项移到别构酶的[S]一项,并且式6?0可看出K'S是随[S]而改变的,不是一个常数。由于K'S的测定是假设V=(1/2)Vm或[S]=S0.5的条件下计算的,故有些作者用S0.5S,来代表别构酶的K'5,以免与Km混淆。